Through The Lens Of A Programmer

Seeing The World As A Programmer

I spend a lot of time talking to computers. That is, if you classify programming a computer as talking to them, which I personally wouldn’t do. If it really were the case that we were talking, then it would certainly be a one-sided conversation.

But it is some form of communication. And if I am stubbornly persistent with trying to personify the computer, which it seems like I am, then it probably would be best described as some form of prescriptive writing. But then again, we could say that programming is a sufficient term.

Anyway, I spend a lot of time programming computers. It is my job to communicate things to a computer in a way that these simple machines will understand. And I do mean simple in a hurtful, nasty way.

“Computers are incredibly fast, accurate and stupid; humans are incredibly slow, inaccurate and brilliant; together they are powerful beyond imagination.”

– quote often misattributed to Albert Einstein

This communication between human and computer involves translating real world problems and objects into a language that a computer can make sense of. This process has impacted the way that I look at the world. Whether I like it or not, I see the world through the lens of a programmer.

But this is a pretty normal thing, right? Our careers have a big impact on how we see the world.

An elementary school teacher might find themselves interpreting the world with the perspective of a small child. They might incorporate more imagination, innocence, or bathroom humor into their day-to-day interactions as a result.

But to take this elementary school teacher comparison a little further, have you ever heard the sentiment, “if you can’t explain it simply, you don’t understand it well enough”? (This quote also gets misattributed to Einstein???) Regardless, there seems to be a nugget of truth in that statement.

A good grasp of a concept, along with a certain degree of tact, is required when explaining simply a complex idea.

If Einstein were an elementary school teacher and one of his students, little Oskar, asked, “Mr. Einstein, what is General Relativity?”, then Einstein would have to simplify his idea, which would involve tossing aside a great deal of essential information about what General Relativity is and how it works.

The paraphrasing that happens when Mr. Einstein explains General Relativity to his elementary school class, I would argue, is not too dissimilar from the process that programmers participate in when explaining problems to a computer.

It involves understanding your audience (a child, or a computer), and maybe even “thinking” like them, as well as using a form of language that they will understand. It also requires figuring out which parts are more important and which might not be as important.

I guess it could be said,

”If you can’t decompose something into a series of basic instructions that a computer would understand, then you don’t understand it well enough.”

– Albert Einstein, probably

Done frequently enough, I think this process gives us a new perspective—we are able to add a new lens to our proverbial glasses, through which we can better understand the world.

When I’m feeling like an optimist, I like to think that this career helps me understand the world around me just a little bit better, in my own unique way.

This is a sort of case study of that process.

The Noticing Step

It starts with, perhaps, noticing. Something. Anything.

In this case, a natural phenomenon of how light behaves when it passes through a curved surface.

I was on vacation and at a bar in Ocracoke, North Carolina, an island off the coast of the Outer Banks, and I noticed the light passing through my drink and onto the countertop.

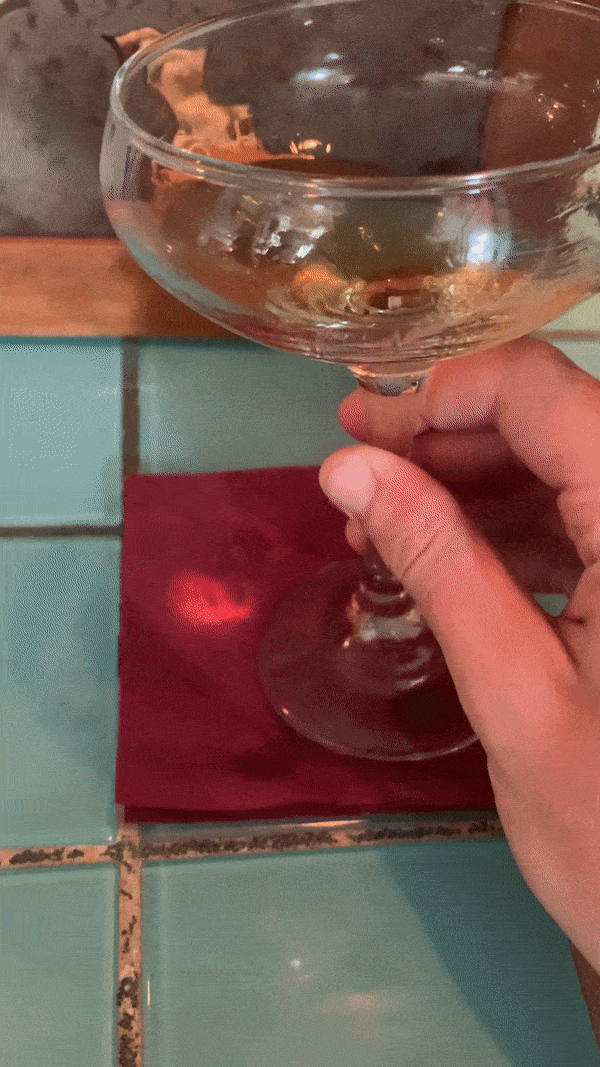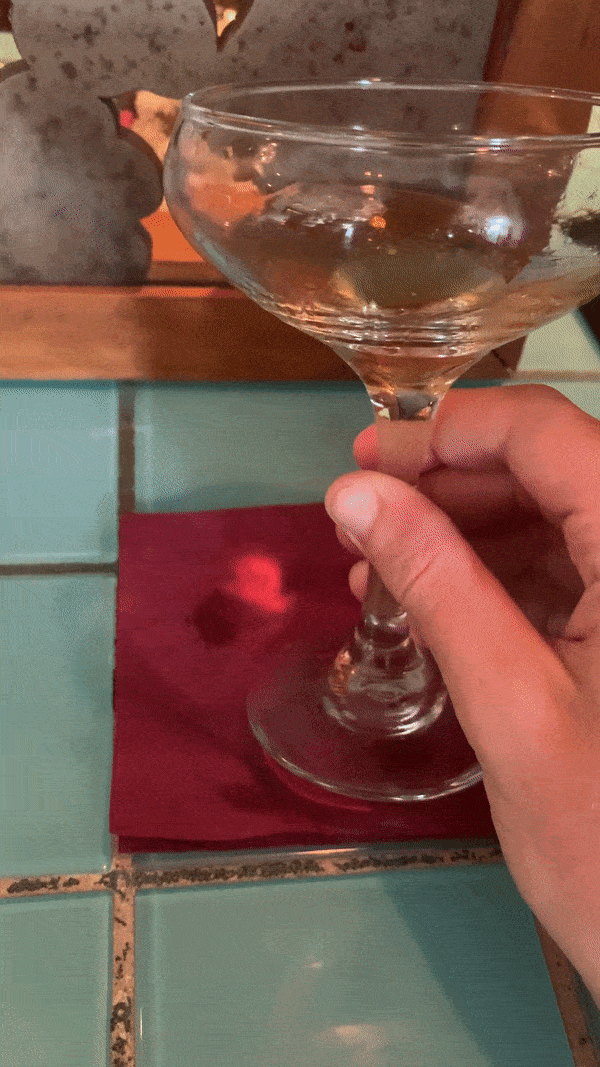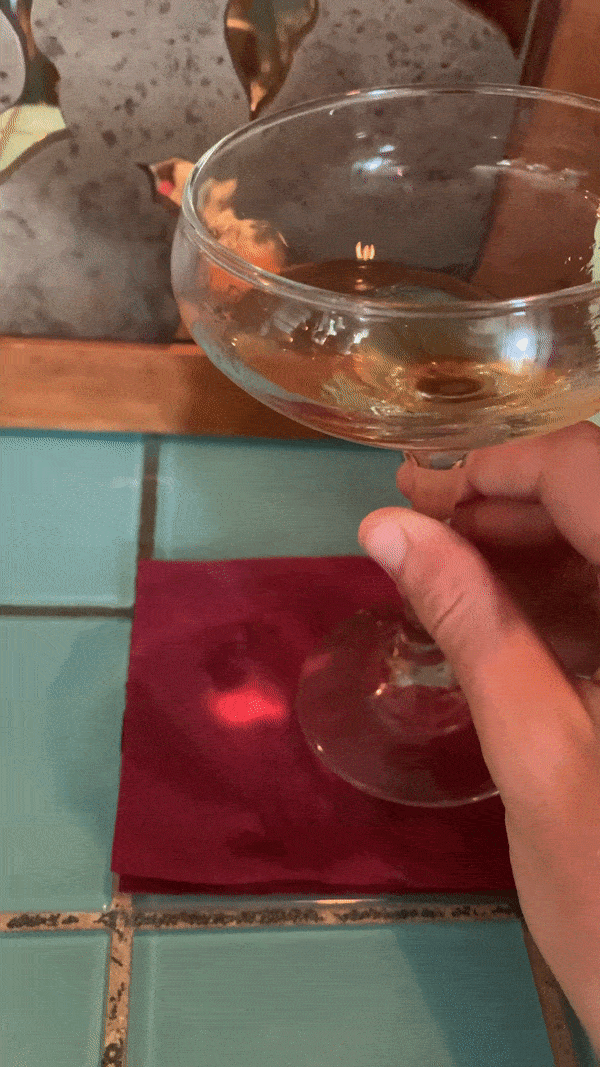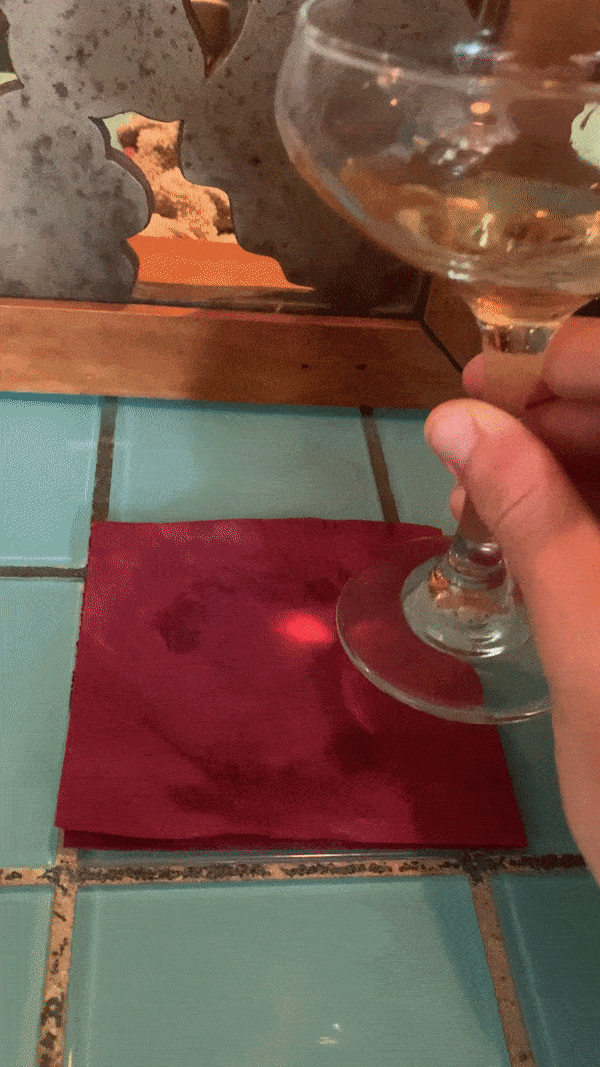
Sometimes the initial observation isn’t enough. It’s missing something. A little reinforcement.

Later that same day, I stumbled upon a YouTube video on how light being refracted through curved surfaces (caustics) is the hardest visual effect to produce.

Caustics. I had never heard the word before, but after this serendipitous, coincidental series of events I was officially intrigued.

The Scientific Step: What Are Caustics

“Caustic” can mean a couple different things, but what I’m interested in right now is caustics as they relate to the study of sight and the behavior of light.

The word caustic comes from the Greek καυστός, burnt, which itself is from the Latin causticus, a.k.a., burning, which when related to optical caustics refers to the capability of focused light as seen below.

https://www.flickr.com/photos/spacepleb/1505372433

When light passes through a curved object, the rays of light are redirected and, in the extreme example of a magnifying glass held at the right angle, the light can be concentrated to a very bright point.

In the above example you can see the bright spot. But also, let’s not forget the underappreciated shadow, which is the byproduct of the light being redirected to a point. Pretty cool if you ask me.

This phenomenon on a large scale caused quite some problems in London in 2013, where a skyscraper shaped with a nice concavity was reflecting light and melting cars when the sun hit it just right.

As a less dramatic example, take light passing through a wine glass. The same principle is occurring—light is being refracted by a curved surface.

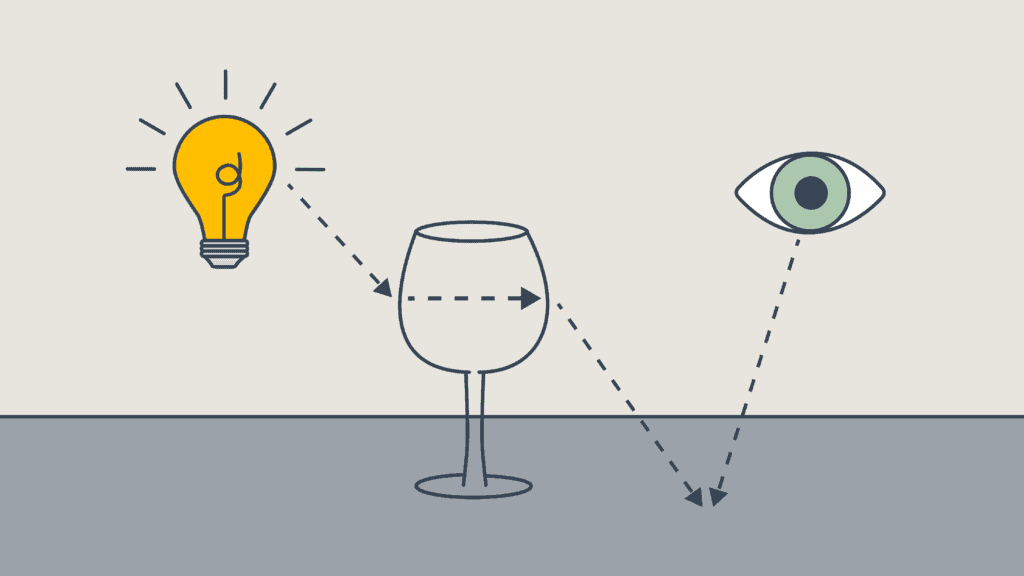
As the light passes through the wine glass, a focusing and shadowing occurs which is less perfect than the magnifying glass, but impressive nonetheless. The resulting caustics are such a common encounter for us that frankly I think we’re mostly immune to noticing them. I certainly am.

https://www.flickr.com/photos/spacepleb/1505372433

But, again, my interest in caustics (besides their aesthetic beauty), is through the lens of a programmer.

In caustics, I found a concept which I knew very little about, which represented a challenge to better understand the world around me, and which might even help me pick up a few skills or new technologies along the way.

We’ve already covered how caustics work in the real world, which is one step closer to recreating them.

The Programmer’s Step

The programmer’s step, summed up as a question, might be, “How would a computer understand this?”

More targeted questions might sound something like…

• How can we represent this concept mathematically?
• How can we represent the concept in a language that a computer might understand?
  • Can we do this efficiently?

• What techniques are people currently using to represent this concept digitally?
• What processes, transformations can we tell the computer to perform on our data?
• How can we output our data?
  • Image, sound, text, video?

Note that I tried to generalize these questions, so some of them might sound silly or trivial when we apply them to caustics. For example, with the last question “How can we output our data?”—it seems most fitting that since caustics are an optical phenomenon, we should output our caustics as a rendered image or video.

I.e., something like this:

https://en.wikipedia.org/wiki/File:Computer_rendering_of_a_wine_glass_caustic.png

But, just as an exercise in creativity, if we imagine what else we could do with our caustic data, we might come to realize that it’s possible to apply a lot of the same basic ideas behind caustics to acoustics! This opens the door for a lot of cool applications, like applying visuals to a song, or simulating what a 3D space might sound like (auditoriums, restaurants, airplanes, etc.).

There’s even such a thing as acoustic shadows, which I learned about while researching for this article, and I just think that’s so cool.

The Rubber Hits The Road Step: Ray Tracing

One of the most important ideas that we have to first understand if we’re going to understand caustics as a computer might understand them is ray tracing.

There are other rendering methods (path tracing, scanline rendering, etc.), but ray tracing is the most common method, and one of the easier ones to understand, so I’m going to keep my focus here for this article.

Now, I’m going to wait just a little bit longer to properly define ray tracing. First I want to give some background so that our definition will make a little more sense.

Ray tracing introduces a couple new concepts that I had not heard before in this context:

• The camera, or a virtual point of view, or an imaginary eye, or the eye point
• The image, or the virtual screen, or the viewing plane
• The scene
  • Scene object(s)
  • Light source(s)

Ray tracing can trace its rays history back to 1525(!), when Albrecht Dürer, a German painter, created a perspective drawing device known today as Dürer’s Door.

https://upload.wikimedia.org/wikipedia/commons/1/1a/D%C3%BCrer_-_Man_Drawing_a_Lute.jpg

This analogue version of ray tracing follows the same principles of ray tracing that a modern 3D rendering software employs. The camera is analogous to the hooks on the wall, the rays are the string, the scene object is the lute, and the image is the paper pinned to the door (where you can see the dotted line drawing of the lute).

It helps me to look at Dürer’s Door and compare it to this schematic below.

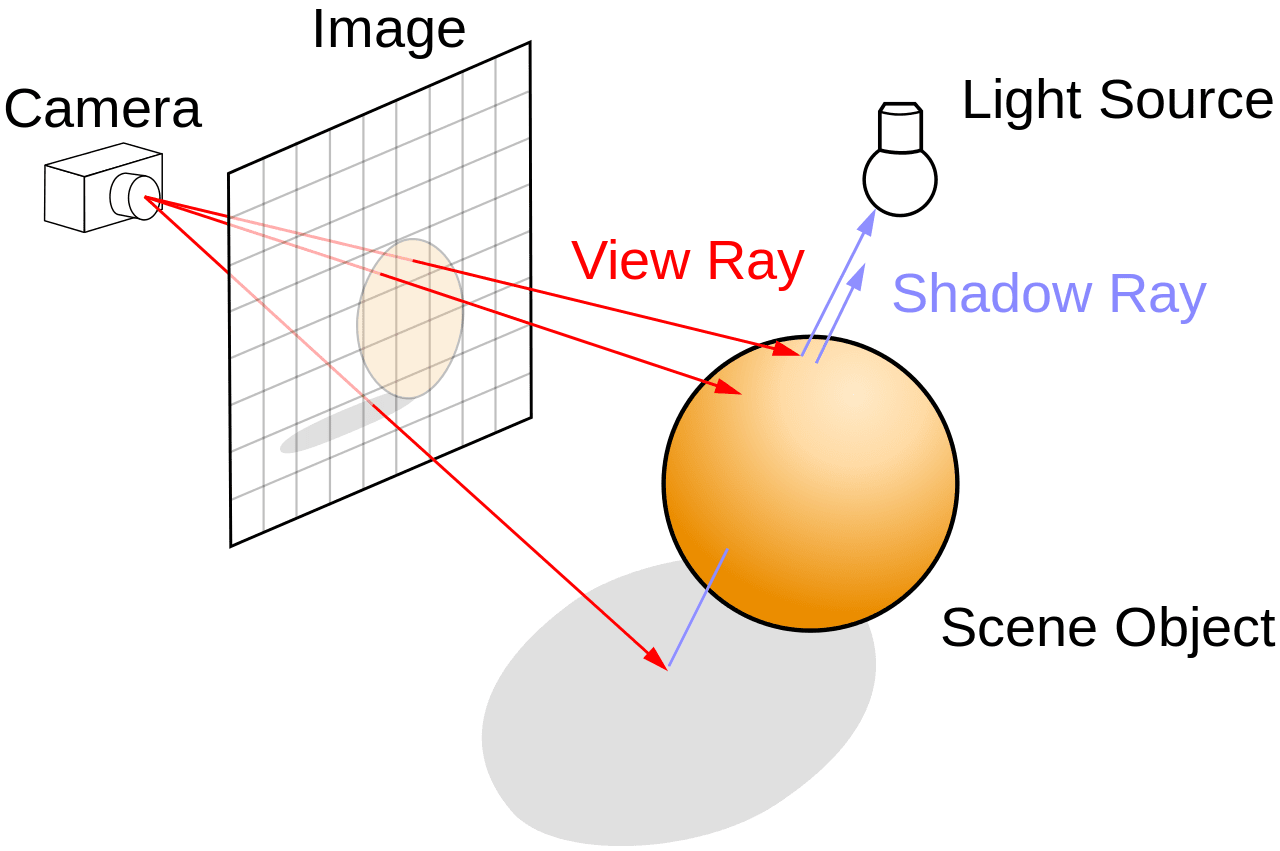
https://upload.wikimedia.org/wikipedia/commons/thumb/8/83/Ray_trace_diagram.svg/1280px-Ray_trace_diagram.svg.png

Technically Dürer’s device more closely resembles ray casting, than ray tracing.

So, back to the definition.

Ray tracing is an algorithm which utilizes ray casting as its first step, and then continues to calculate secondary rays after they have been reflected or refracted, then tertiary, and so on, until some halting condition is met.

So where ray casting is limited to certain geometric objects, and would only ever be able to give us an outline of a lute, or the outline of a wine glass, ray tracing can reveal the reflection on a lute’s glossy surface, or dare I say, the caustics from light passing through a wine glass.

The Rubber Hits The Road Step, Part II: Reflecting and Refracting

One of the key new players in ray tracing is the reflecting and refracting. This didn’t matter in ray casting since the algorithm stopped after the rays hit the object. But now that we’re tracking the bouncing of light, we need to tell the simulated light how exactly it’s supposed to respond.

Different objects interact with light differently.

Some objects, like our wine glass, are translucent, which means the light is going to pass through it and potentially be refracted. How much refraction occurs will depend on the refractive index. The refractive index of glass is about 1.5, which actually means light moves 1.5 times slower in glass than when it’s moving at its fastest, through a vacuum.

This means that for each ray of light, we need to calculate the angle and where it hits the curve of the wine glass, and apply the refractive index. This gets pretty complicated, but the most common way these calculations are done is with a refraction map. Further technical reading on refraction if you’re interested:

• Nvidia
• Autodesk

Other objects are opaque. For opaque objects we use Bidirectional Reflectance Distribution Functions, or, more commonly, BDRF’s.

A BDRF is a way to represent the diffuseness or glossiness of a material, mathematically.

Diffuse Object

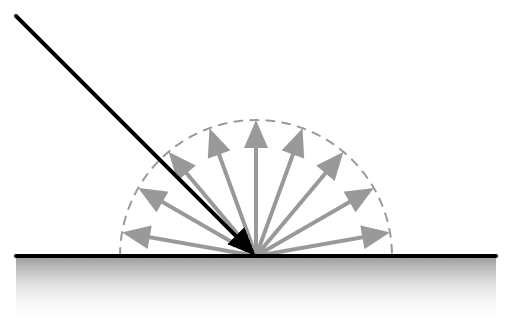
https://en.wikipedia.org/wiki/File:BRDF_diffuse.svg

Glossy Object

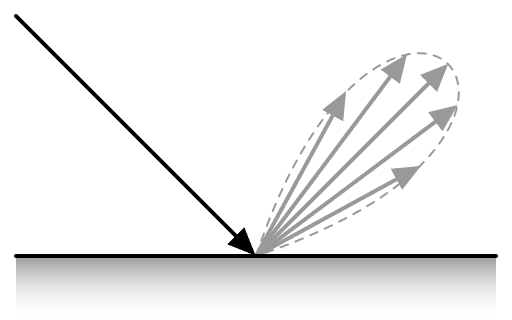
https://en.wikipedia.org/wiki/File:BRDF_glossy.svg

Mirror-like Object

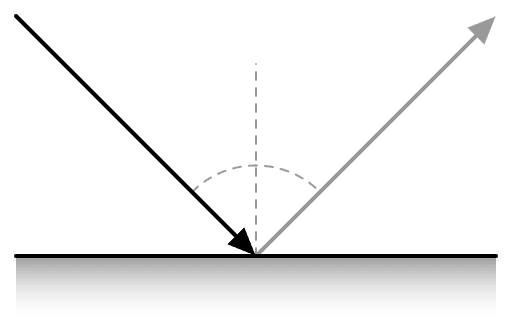
https://en.wikipedia.org/wiki/File:BRDF_mirror.svg

After learning about refractive indexes and BRDF’s, I can’t help but look at the things around me a little bit differently. I like to imagine the light passing through the window slower, or how the things in my house might be reflecting or diffusing rays of light.

The Considerations

Caustics, refraction maps, and other ray tracing related calculations take a lot of computing power. It’s particularly difficult to perform these calculations in real time.

Generally, when a calculation is too expensive, we find a workaround. This means we might no longer stay true to physically based rendering, a.k.a., simulating the way that light behaves in the real world.

For example, the caustics of light shining through water and onto the bottom of a pool can be “faked” by just projecting an animated image on a loop. The results can look pretty believable.

Another method is to perform some sort of approximation.

One of the coolest examples of caustic approximation that I’ve come across is Evan Wallace’s water simulation, which runs in real time in the browser (using WebGL). He wrote about how he made it here.

I highly recommend checking the water simulation out. It works best on desktop, but you can get the gist on mobile as well.

Screenshot from Evan Wallace’s water simulation

The Aftermath

So we’ve broken down a topic through the lens of a programmer.

Together with ray casting, calculating where the casted rays intersect with objects and where they bounce, up to some number of bounces, we can render a fairly realistic 3D image.

It’s that easy! Well, easy isn’t exactly the right word, but we can see that all of the concepts broken down are actually simple enough.

What now? There’s a lot more to learn, and we haven’t actually programmed anything.

Writing our own ray traced caustics from scratch would be… quite the endeavor. Something I want to take on, but not in this blog post.

Instead, for the sake of brevity and everyone’s sanity, I chose to focus more on the methodology and not the actual programming. Which, really, truly, and honestly, is a more realistic depiction of how this process plays out.

For me, it isn’t about sitting down and programming a 3D image rendering software. It’s more so about walking around and noticing the caustics around me—imagining the little rays of light refracting and reflecting off of objects, and having a little bit better of an understanding and a little bit more appreciation of the details around me.