Immutability and tail recursion

I was in Amanda Laucher’s F# talk yesterday and I asked about whether F# was able to tell if a function was pure or semi-pure. (A pure function is simply a function with no side effects, and a semi-pure function is one that only modifies locals) I was just a bit curious if F# was able to tell if there were any immutable variables that had been introduced into method, or if any mutable variables had been changed during a method. Well, I got my answer and then I made a statement that I probably definitely should have shut my mouth on. I essentially asked if introducing mutable variables would cause the F# compiler to not do its tail recursion optimization.

Yeah, I don’t know what I smoked that morning. So, if you know all about tail calls and tail recursion optimization, then feel free to stop reading now. Otherwise, you can continue on to learn just how dumb of a statement that was. First of all let me just say that I have actually found a few blog posts where people have made the same mistake, and that makes me feel at least a *bit* better. I guess it is the fact that tail recursion optimization is usually associated with functional languages, since they mostly do looping with recursion, you would run into a lot of problems with even relatively small loops if you couldn’t find a way to remove the recursion. But that doesn’t really excuse me for not thinking about my question before I asked it.

So, anyways, we all know what recursion is. It is just when a method calls itself (below is direct recursion, there is also indirect recursion. I can’t find a good link for a definition, so suffice to say that indirect recursion is when method A calls method B which in turn calls back to method A. More than two methods can be involved, but they don’t have to be.)

static void increment(int n)

{            

    increment(n + 1);

}

Now, that method is infinitely recursive because we have no base case, but it is recursive nonetheless.

Some of us probably know what a tail-call is, it is when we make a call to a method at the very end of another method:

static void Method1()

{

    int i = 1 + 2;

    Method2();

}

static void Method2()

{

    Console.WriteLine("hello");

}

There are some optimizations that can be made when we are doing a tail call, mainly due to the fact that we can reuse the stack frame of the method we are calling from, since it is no longer needed. (Since there are no instructions after our method call).

Well, there is a little thing called tail recursion as well. And tail recursion is when your recursive call is a tail call. Our “increment” method above is actually tail recursive, since we are calling increment at the end of the method and there is nothing after it. But this method would be considered tail recursive as well:

static void increment(int n)

{            

    if (n > 500000000)

    {

        Console.WriteLine(n);

    }

    else

    {

        increment(n + 1);    

    }    

}

And you may even be surprised to know that this is considered tail recursive, since after increment nothing else will ever be called.

static void increment(int n)

{                

    if (n > 500000000)

    {

        Console.WriteLine(n);

    }

    else if (n > 1000000)

    {

        increment(n + 2);

    }

    else

    {

        increment(n + 1);    

    }    

}

To make it more clear, look at this in IL:

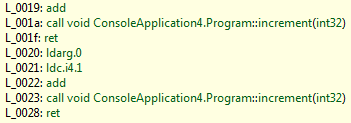
Now you can see that after each call to “increment” we are going to return. This way it is easy for the compiler to tell this is the last instruction we are going to execute. Now, the beauty of tail recursion, is that since the recursion happens at the end of our method, we can essentially eliminate the recursion by using a loop. This is why (as Amanda showed us in her F# presentation) the F# compiler will turn our original increment method into something that looks like this:

static void increment(int n)

{                

    while (true)

    {

        n++;

    }    

}

And when you run it in C# our original “increment” method will blow up with a StackOverflowException, right? Well, kinda. So, lets build our app and run it under Debug mode. Well, we quickly get this:

But, like a good programmer, we know that running things in Debug mode often disables many compiler optimizations. Sooooo, we change our build type to “Release” and try it again. Suddenly our app is now running, happily pegging one of my CPU’s…

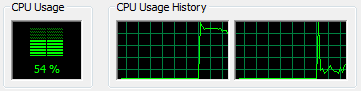
What is that you say? On your machine you still got a StackOverflowException? Well, maybe you should get a new machine, I think yours is broken! Ha ha, just kidding! There is a mystery afoot. What happened on my release build, that you are not seeing on your machine? Or maybe you are seeing it? Well, it happens that I am running Vista 64-bit, and if you are seeing this app run fine as well, then you too are running on 64-bit hardware. (In order to prove this to yourself if you are running on a 64-bit machine, you can switch your target CPU to x86, then run in release mode and the StackOverflowException will appear quite quickly!!)

As a side note, after I ran this and realized that I was getting tail recursion optimization, I set about to find out why. Since I did not write the .net runtime (although it would be cool if I did) I had to rely on info from a few different places, but a great one was this post by Jomo Fisher. A lot of the info below this point was gleaned from his post!

But why should that make any difference? Well, let us take a look at our compiled IL:

64-bit:

32-bit:

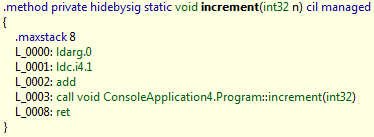
Hmmm, they look the same… I thought you said that the 64-bit release would optimize our tail recursion? Well, you have to remember that in managed code there is more than one chance for optimization. Optimizations can occur at build time when the IL is generated (hence what F# is doing) and optimizations can also be done by the JITer (Just In Time compiler) when the code is turned from IL into native machine code (which the 64-bit JITer is doing for us).

In order for us to tell that this is actually happening, lets add some code at the end of our method in order to stop the JITer from optimizing our tail recursion and see if we can get our StackOverflowException. So we add this change:

static void increment(int n)

{                    

    increment(n + 1);

    int i = 5;

    i = i + 2;

}

I had to add the second line because just putting in “int i = 5;” the compiler was smart enough to optimize it out because it wasn’t being used. Tricky compiler. So, now that we have made this change our application now blows up with a StackOverflowException even when running under the 64-bit JITer!

So there you go, you can now see that tail recursion is completely useless in C#! Since the optimization is done by the JITer and not by the compiler, the code above will run on 64-bit machines, but will crash quickly on 32-bit machines. These are the stuff that nightmares are made of. Anyways, the F# compiler obviously had to do these optimizations for itself since tail recursion is much more prevalent in functional languages and they can’t assume that you’ll always be running under a 64-bit OS. Although you SHOULD be!

And with that, we are back to my original point for this article. Immutable types and tail recursion optimization have nothing to do with each other. There are some other optimizations that can be done when a method is pure (such as automatic parallelization), but nothing to do with tail recursion. Well, at least nothing that I could find, so please prove me wrong! Hope you enjoyed this post, and hopefully you aren’t laughing at me too hard right now. 🙂