
I recently put up a post on my blog about some of the new concurrent collections in .NET 4.0, and I noticed that a lot of people were being sent by Google to those posts who were only searching for System.Collections. I figured that maybe people could use a similar overview of the collections available to them in the System.Collections.Generic namespace, since it seems to me that no one uses anything other than List and Dictionary. So, in this post, I am going to take a look at a few of those collections, and explain exactly why you would want to use them.
Keep in mind as you read through this list that you shouldn’t just start switching out collection types in code that you already have working. If something is working and performing properly for you, it is almost always better to take the easier route until you have proof that the easy approach does not work for you.
System.Collections.Generic.List<T>
The first collection that we are going to look at is List<T>. Like I said before, this collection seems to be the fallback, and with good reason. It is unsorted (but supports sorting), items can be added, removed, or inserted at a specific index. It also has indexed access, meaning that items can be accessed directly using a numeric index. You can add Ranges, perform binary searches, perform sequential searches, built in sorting, get the count of items, check for items within it, pass a delegate to it to perform actions, etc… It really is the Swiss Army knife of collections.
In computer science we know that there are always trade-offs. Nothing comes for free, and in order to have the ability to perform operations like indexed lookups, we need to have some kind of data structure which will support this ability. Because of this, List<T> is internally implemented as a simple array. And as we add more and more items to the list, if the array fills up, then an entirely new array is allocated and the items in the current array are copied over into the new array, and the new item is added:
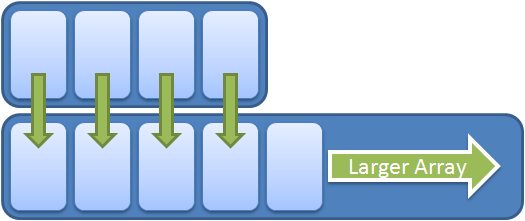
The default length of the array inside of a List<T> is 4, and it only doubles in size each time it fills up (so it goes 4, 8, 16, 32….), so if you know that you have a really large number of items to pass to the list, then you should probably consider using the constructor that allows you to tell the List<T> what size to start off at. It will really keep you from having to copy a lot of data around.
Most of the operations are really straight forward, and looking at the operations below, you can probably see why List<T> is the generic fallback for any list of unknown length, it provides good performance across a very wide variety of operations.
Examples of most common operations:
var list = new List<string>();
list.Add("one");
list.Add("two");
list.Add("three");
list.AddRange(new[] {"four", "five", "six"});
//insert item at index 2
list.Insert(2, "seven");
//removes first occurrence of "seven"
list.Remove("seven"); //returns true
//removes all occurrences of "seven"
list.RemoveAll(s => s == "seven");
//checks is list contains two
list.Contains("two"); //returns true
//finds the first item which matches predicate
string value = list.Find(s => s == "three");
//finds all items which match predicate
List<string> values = list.FindAll(s => s == "three");
//gets a range of the list
List<string> range = list.GetRange(2, 3);
//in-place sort of list
list.Sort();
//performs a binary search of a sorted list to find index of item
int index = list.BinarySearch("three"); // must sort first!
//removes all elements
list.Clear();
| Bottom Line: | |
| Add | Very Fast – O(1) |
| Inserts | Average – O(N) |
| Lookup | Average – O(N) |
| Sorted Lookup | Fast – O(log N) – must sort first |
| Delete | Average – O(N) |
| Versatility | High |
System.Collections.Generic.SortedList<TKey,TValue>
SortedList is very similar to List, with one obvious difference, it is sorted. In order to add an item, you have to provide a sort key and a value, which are both stored. A binary search is performed across the list in order to find the right place to insert the item, and then the item is inserted into the array. In order to do this, the entire array has to be shifted in order to make room for the new item:
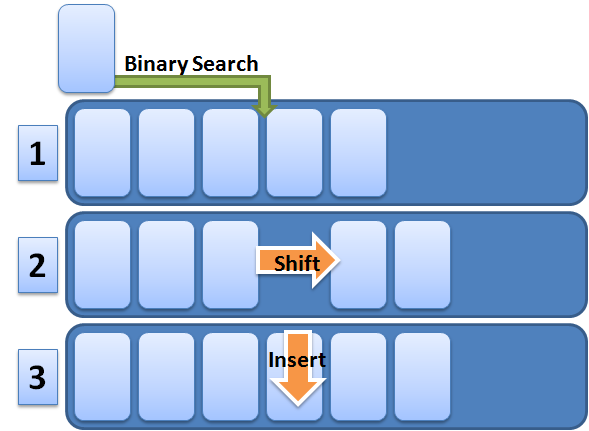
Due to this, inserting items into the SortedList is an expensive operation. But because the list is maintained as sorted, lookups are very cheap. Because you need both a key and a value, you must provide these on most operations. Since lookups are so cheap, if you need a list which will have heavy lookups with a lower number of inserts, then the SortedList may be a good option for you.
Example of most common operations:
var sortedList = new SortedList<int, string>();
sortedList.Add(1, "one");
sortedList.Add(2, "two");
sortedList.Add(3, "three");
sortedList.Add(4, "four");
// returns true
sortedList.ContainsKey(1);
// returns true
sortedList.ContainsValue("two");
// get index of key
sortedList.IndexOfKey(1);
// get index of value
sortedList.IndexOfValue("two");
// remove by key
sortedList.Remove(3);
// remove by index
sortedList.RemoveAt(2);
// lookup by key
string value = sortedList[2];
// get value by index
string value = sortedList.Values[2];
// get key by index
int key = sortedList.Keys[2];
string value;
if (sortedList.TryGetValue(4, out value))
//do something
foreach (int key in sortedList.Keys)
{
Console.WriteLine(key);
}
foreach (string value in sortedList.Values)
{
Console.WriteLine(value);
}
//removes all elements
sortedList.Clear();
| Bottom Line: | |
| Add | Average – O(N) |
| Inserts | Average – O(N) |
| Lookup | Average – O(N) |
| Sorted Lookup | Fast – O(log N) -presorted |
| Delete | Average – O(N) |
| Versatility | Medium |
System.Collections.Generic.Dictionary<TKey,TValue>
The next collection that we are going to look at is the Dictionary. The Dictionary class is an implementation of a dictionary data structure (sometimes referred to as an associative array or a map). Its operations look very similar to a SortedList, since it takes both a key and a value, but in reality they have very different performance characteristics.
The reason for this is that while a SortedList performs an insertions and lookups using a binary search, the Dictionary class actually uses a hash table as its backing store. This means that the data stored inside of the dictionary isn’t sorted, it is looked up by a hash value (meaning that the keys must also be unique). This allows for individual items to be looked up extremely quickly by hashing it, and then looking up its hash inside the hash table:
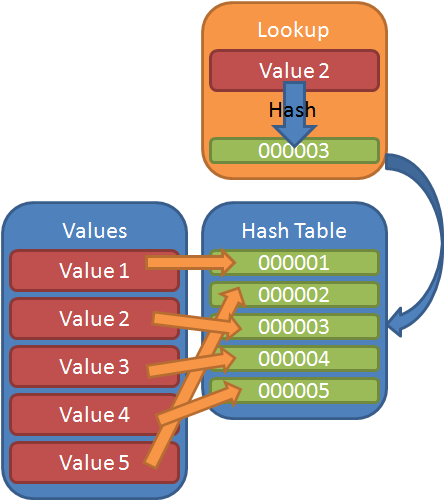
Because of this, finding a range of values would require you to iterate over all of the values in the dictionary and look for your values. It also means that the data stored in the Dictionary, when iterated over, comes back in an non-determinant order (currently this appears to be in inserted order, but don’t rely on that because it could change at any time) and not in a sorted order.
Example of most common operations:
var dictionary = new Dictionary<int, string>();
dictionary.Add(1, "one");
dictionary.Add(2, "two");
dictionary.Add(3, "three");
dictionary.Add(4, "four");
// returns true
dictionary.ContainsKey(1);
// returns true
dictionary.ContainsValue("two");
// remove by key
dictionary.Remove(3);
// lookup by key
string indexedValue = dictionary[4];
string value;
if (dictionary.TryGetValue(4, out value))
//do something
foreach (int key in dictionary.Keys)
{
}
foreach (string value in dictionary.Values)
{
}
//removes all elements
dictionary.Clear();
| Bottom Line: | |
| Add | Average – O(1) |
| Inserts | Not applicable, data isn’t in any order |
| Lookup | Average – O(N) |
| Indexed Lookup | Fast – O(1) |
| Delete | Fast – O(1) |
| Versatility | Low |
System.Collections.Generic.SortedDictionary<TKey,TValue>
In all likelihood, you have probably never used a SortedDictionary. You might not even know what in the world a SortedDictionary is, or why it would be any different from a SortedList. You might also be thinking that it doesn’t really make any sense to have a sorted dictionary since the idea of a dictionary is to provide indexed lookup of items. So where does this leave the SortedDictionary?
Well, the SortedDictionary is actually quite a different beast. Internally it is implemented as a Red-black tree. Red-black trees are a much more complicated data structure than what we have looked at so far, so I’ll just give you a link to the Wikipedia page on Red-black trees. What is important to know about Red-black trees is that they have very good worst-case operations.
The biggest difference between this and a SortedList is that the SortedDictionary doesn’t allow indexed access. It does however have faster add, insertion, and deletion times. Also, because of the tree structure in which the data is stored, the SortedDictionary uses more memory than a SortedList.
Example of most common operations:
var sortedDictionary = new SortedDictionary<int, string>();
sortedDictionary.Add(1, "one");
sortedDictionary.Add(2, "two");
sortedDictionary.Add(3, "three");
sortedDictionary.Add(4, "four");
// returns true
sortedDictionary.ContainsKey(1);
// returns true
sortedDictionary.ContainsValue("two");
// remove by key
sortedDictionary.Remove(3);
// lookup by key
string value = sortedDictionary[2];
string value;
if (sortedDictionary.TryGetValue(4, out value))
//do something
// sorted by key
foreach (int key in sortedDictionary.Keys)
{
Console.WriteLine(key);
}
// sorted by key
foreach (string value in sortedDictionary.Values)
{
Console.WriteLine(value);
}
//removes all elements
sortedDictionary.Clear();
| Bottom Line: | |
| Add | Fast – O(log N) |
| Inserts | Fast – O(log N) |
| Lookup | Not Applicable |
| Sorted Lookup | Fast – O(log N) |
| Delete | Fast – O(log N) |
| Versatility | Low |
System.Collections.Generic.LinkedList<T>
The LinkedList class is an implementation of a doubly linked list data structure. A doubly linked list is a fairly simple data structure consisting of a bunch of nodes with pointers to the previous and next node:
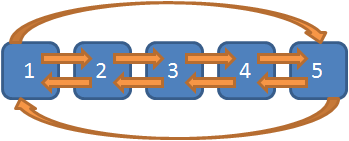
The .Net Framework implementation also point the next and previous pointers on the first and last item to each other. Because of the way that this data structure works, it makes it very cheap to add and insert items, assuming that you are already in the place in the list where the data needs to be inserted. In order to insert a node, the pointers merely need to be redirected:
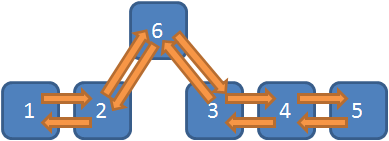
Also, since pointers only exist between nodes, there is no indexed access and it in order to find items in the list, each item needs to be iterated through.
The LinkedList may be a simple data structure, but it is an excellent data structure if you have a list which has a heavy amount of insertion and deletion within the list. It is especially useful if you are inserting ranges of data into the middle of a list.
Example of most common operations:
var linkedList = new LinkedList<string>();
// add node to front of list
linkedList.AddFirst("one");
// add node to end of list
var nodeThree = linkedList.AddLast("three");
// add node before given node
linkedList.AddBefore(nodeThree, "two");
// add node after given node
linkedList.AddAfter(nodeThree, "four");
// iterate list printing one, two, three, four
foreach (string value in linkedList)
{
Console.WriteLine(value);
}
// find first node with value "two"
var nodeTwo = linkedList.Find("two");
// find last node with value "three"
nodeThree = linkedList.FindLast("three");
// get first node in list
var firstNode = linkedList.First;
// get last node in list
var lastNode = linkedList.Last;
// remove the first node with value "two"
linkedList.Remove("two");
// remove first node in list
linkedList.RemoveFirst();
// remove last node in list
linkedList.RemoveLast();
// remove all items from list
linkedList.Clear();
| Bottom Line: | |
| Add | Very Fast – O(1) |
| Inserts | Very Fast – O(1) |
| Lookup | Slow – O(N) |
| Sorted Lookup | Not Applicable |
| Delete | Very Fast – O(1) |
| Versatility | Low |
System.Collections.Generic.SortedSet<T>
SortedSet is new to .NET 4.0. It is actually the backing store for the SortedDictionary data type, but unlike the SortedDictionary there is only values and no keys. Also, the SortedSet exposes some set operations unlike the SortedDictionary. Since it is the backing store for the SortedDictionary it has the same performance characteristics.
The SortedSet represents a set abstract data structure. A set is a collection that contains unordered unique values. It is an abstract data structure because a set does not imply any particular implementation. This implementation uses a Red-black tree, which is a sorted data structure, in order to maintain the rules of the set. While technically a set does not have any order, this is a sorted set, and therefore if you iterate over all of the items within the set they will be in sorted order.
The SortedSet is best used when you are storing a unique set of values which need to be sorted and which might require ranged lookups, or other set based operations (intersects, unions, etc…).
Example of most common operations:
var sortedSet1 = new SortedSet<string>();
sortedSet1.Add("one");
sortedSet1.Add("two");
sortedSet1.Add("three");
sortedSet1.Add("four");
var sortedSet2 = new SortedSet<string>();
sortedSet2.Add("two");
sortedSet2.Add("four");
sortedSet1.Contains("three");
// sortedSet1 now contains one, three
sortedSet1.ExceptWith(sortedSet2);
// sortedSet1 now contains two, four
sortedSet1.IntersectWith(sortedSet2);
// a subset is a set whose elements are all in
// another set
sortedSet1.IsSubsetOf(sortedSet2);
// a superset is a set which contains all elements
// in another set
sortedSet1.IsSupersetOf(sortedSet2);
// a proper subset is a subset which is not equal
sortedSet1.IsProperSubsetOf(sortedSet2);
// a proper superset is a superset which is not equal
sortedSet1.IsProperSupersetOf(sortedSet2);
// returns bool if both sets contain any of the same items
sortedSet1.Overlaps(sortedSet2);
// removes the element with value "two"
sortedSet1.Remove("two");
// removes all elements that match the predicate
sortedSet1.RemoveWhere(v => v == "three");
// returns true if both sets are identical
sortedSet1.SetEquals(sortedSet2);
// sortedSet1 now contains one, three
// only items which are in one or the other, not both
sortedSet1.SymmetricExceptWith(sortedSet2);
// sortedSet1 now contains one, two, three, four
// all items in both sets
sortedSet1.UnionWith(sortedSet2);
// returns all items between the given values
SortedSet<string> result = sortedSet1.GetViewBetween("two", "four");
// elements are in sorted order
foreach (string value in sortedSet1)
{
}
// remove all items in both sets
sortedSet1.Clear();
| Bottom Line: | |
| Add | Fast – O(log N) |
| Inserts | Fast – O(log N) |
| Lookup | Not Applicable |
| Sorted Lookup | Fast – O(log N) |
| Delete | Fast – O(log N) |
| Versatility | Medium |
System.Collections.Generic.HashSet<T>
HashSet is another set data structure that uses hashes in order to maintain a unique set of items. Internally the items are stored in an array, which requires expansion when the array fills up. The hash table size is increased to each subsequence prime number in size as the buckets fill up (this is done because some hash functions will only evenly hash values if the number of available buckets is prime).
Because hashes are used as a backing store, the data is unsorted, which means that finding ranges is an O(N) operation since all data would need to be searched through. At the same time, hashes are very fast with insertions and lookups and so performing set operations such as unions, intersects, etc… could be much faster on a HashSet than a SortedSet. Keep in mind that inserting can cause the array to be expanded, which would cause the operation to be much more expensive.
Since HashSet and SortedSet both implement ISet, the only real reason to use SortedSet is if you have data that you might need to look up in ranges or if you have data which cannot be easily hashed. If neither of those applies to your situation, then the HashSet will probably be the faster of the two sets to use, and it will use less memory.
Example of most common operations:
var hashSet1 = new HashSet<string>();
hashSet1.Add("one");
hashSet1.Add("two");
hashSet1.Add("three");
hashSet1.Add("four");
var hashSet2 = new HashSet<string>();
hashSet2.Add("two");
hashSet2.Add("four");
hashSet1.Contains("three");
// sortedSet1 now contains one, three
hashSet1.ExceptWith(hashSet2);
// sortedSet1 now contains two, four
hashSet1.IntersectWith(hashSet2);
// a subset is a set whose elements are all in
// another set
hashSet1.IsSubsetOf(hashSet2);
// a superset is a set which contains all elements
// in another set
hashSet1.IsSupersetOf(hashSet2);
// a proper subset is a subset which is not equal
hashSet1.IsProperSubsetOf(hashSet2);
// a proper superset is a superset which is not equal
hashSet1.IsProperSupersetOf(hashSet2);
// returns bool if both sets contain any of the same items
hashSet1.Overlaps(hashSet2);
// removes the element with value "two"
hashSet1.Remove("two");
// removes all elements that match the predicate
hashSet1.RemoveWhere(v => v == "three");
// returns true if both sets are identical
hashSet1.SetEquals(hashSet2);
// sortedSet1 now contains one, three
// only items which are in one or the other, not both
hashSet1.SymmetricExceptWith(hashSet2);
// sortedSet1 now contains one, two, three, four
// all items in both sets
hashSet1.UnionWith(hashSet2);
// elements are no in any guaranteed order
foreach (string value in hashSet1)
{
}
// remove all items in both sets
hashSet1.Clear();
| Bottom Line: | |
| Add | Very Fast – O(1) |
| Inserts | Not Applicable |
| Lookup | Average – O(N) |
| Indexed Lookup | Very Fast – O(1) |
| Delete | Very Fast – O(1) |
| Versatility | Low |
System.Collections.Generic.Queue<T>
The Queue is a special purpose data structure which implements a queue data structure. A queue is a FIFO (First In First Out) collection with two main operations: Enqueue and Dequeue. Items are placed into one end of the queue, and then are taken off the other end:

The Queue is really only useful if you need the exact semantics that the queue data structure provides. One reason might be to place work items into the queue and then be able to take the off and process them in order. If you need this kind of functionality, then the Queue is for you. In .NET 4.0 a ConcurrentQueue was also implemented which allows for items to be enqueued and dequeued on multiple threads.
Example of most common operations:
var queue = new Queue<string>();
// pushes an item on the end of the queue
queue.Enqueue("one");
queue.Enqueue("two");
queue.Enqueue("three");
queue.Enqueue("four");
// returns true
queue.Contains("four");
// takes the item off the front of the queue
string item = queue.Dequeue();
// gets the item off the front of the queue
// without removing it
string peekItem = queue.Peek();
// remove all items from the queue
queue.Clear();
| Bottom Line: | |
| Add | Very Fast – O(1) |
| Inserts | Not Applicable |
| Lookup | Average – O(N) |
| Sorted Lookup | Not Applicable |
| Delete | Very Fast – O(1) – Only from end. |
| Versatility | Very Low |
System.Collections.Generic.Stack<T>
The Stack is another special purpose data structure which implements a stack data structure. A stack is a LIFO (Last In First Out) collection with two operations: Push and Pop. Items are placed on the top of the queue and then are taken off the top:
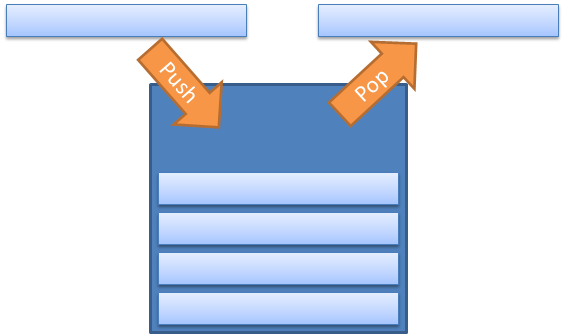
Again, the Stack is a special purpose data structure that has applicability only within a subset of problems. In .NET 4.0 a ConcurrentStack was implemented which allows you to push and pop items on multiple threads without locking.
Example of most common operations:
var stack = new Stack<string>();
// puts an item on the top of the stack
stack.Push("one");
stack.Push("two");
stack.Push("three");
stack.Push("four");
// removes an item from the top of the stack
string item = stack.Pop();
// gets the item on the top of the stack
// without removing it
string peekedItem = stack.Peek();
// returns true if item is in stack
stack.Contains("two");
// removes all items from the stack
stack.Clear();
| Bottom Line: | |
| Add | Very Fast – O(1) |
| Inserts | Not Applicable |
| Lookup | Average – O(N) |
| Sorted Lookup | Not Applicable |
| Delete | Very Fast – O(1) – Only from end. |
| Versatility | Very Low |
Summary
In addition to the collections that we looked at here, in .NET 4.0 they have also added a new namespace called System.Collections.Concurrent which contains a many thread safe collections for you to use, such as ConcurrentQueue, ConcurrentBag, ConcurrentStack, and BlockingCollection. If you want to find even more useful collections, I recommend that you go check out Power Collections for .NET. I hope you enjoyed this overview of the classes within the System.Collections.Generic namespace.
Loved the article? Hated it? Didn’t even read it?
We’d love to hear from you.




Very useful article – will be pointing newbies to it when appropriate. I often have to relate the same information. Thanks!
One of my favs is the KeyedCollection
http://msdn.microsoft.com/en-us/library/ms132438.aspx
Its great for creating dictionaries from types that have their own identifiers. Also, the KeyedCollection serializes well in every scenario, unlike the Dictionary which won’t go through the XmlSerializer.
@Will KeyedCollection is nice, but unfortunately this post was all about the types in the System.Collections.Generic namespace. Maybe in a future post I’ll cover the System.Collections.ObjectModel namespace.
Very good! Keep up the great work!
wrt Dictionary, you can’t assume anything about insertion order. In fact, they explicitly document this:
"The order in which the items are returned is undefined."
http://msdn.microsoft.com/en-us/library/xfhwa508.aspx
@Jonathan Excellent point. I knew that it was undefined, but merely commenting on the order in which it is actually returned. I’ll fix the post to reflect that the order should not be counted upon. Thanks!
Also, your labels for "Lookup" seem…odd.
For example, you mention that Dictionary lookup is O(N), while "Indexed Lookup" is O(1). I find this distinction…odd.
Key lookup is O(1), Value lookup is O(N).
Similarly if Lookup is supposed to mean "value lookup", then SortedDictionary does have a Lookup value (which you list as "Not applicable"), specifically SortedDictionary.ContainsValue():
http://msdn.microsoft.com/en-us/library/1e4d7b8s.aspx
SortedDictionary.ContainsValue() is O(N).
In general, I find the "Lookup" vs. "Sorted|Indexed Lookup" to be confusing, period. See e.g. SortedSet (Lookup is not applicable?!) It looks like you’re trying to make for a consistent table across key/value collections non-key/value collections, but I think keeping the table consistent leads to more confusion than light.
The "Versatility" ratings also seem odd. Your description of HashSet makes it sound more useful than SortedSet (for performance reasons), yet the versatility rating for HashSet is low, while SortedSet is medium. Huh?
Finally, one thing that might be useful (or completely outside the scope of this post, take your pick 😉 is why one would prefer the sorted collections over the hashed collections.
For example, just looking at the numbers it’s hard to imagine many situations when you would prefer SortedDictionary to Dictionary (e.g. O(log N) addition/lookup vs. O(1) addition/lookup). Unless you absolutely need to keep everything sorted all the time, why would you prefer SortedDictionary? (For that matter, how often do you need to ensure things are always sorted, as opposed to just sorting during e.g. display?)
I’m sure there’s some tradeoff here (e.g. really large collections), but offhand I have no idea what the large-scale performance differences are, so I just default to Dictionary most of the time…
@Jonathan Thanks for the feedback. I was looking for a consistent table across items. And you are right that SortedSet also has Lookup in the same manner as HashSet in that you can iterate over the items looking for a specific value. Perhaps my meaning would be clearer if I put the method for performing this action next to each item.
I was looking at versatility as the variety of operations. I thought SortedSet, because of the ability to get ranges and enumerate in sorted order was more versatile. This measurement was put in there to try to express the functionality outside of performance, which is expressed in the other measurements.
@Jonathan I tried to mention some of the reasons in the post, maybe I didn’t specifically under the SortedDictionary but probably under the SortedSet. Honestly the reason is when you need ordered data. It really comes back to binary search tree versus hash table. You can turn a SortedDictionary into an ordered list in O(n) time, while doing the same with a HashTable would be very expensive. Also, after turning into a list, finding ranges of data in a SortedDictionary is much faster, since all of the key values are sorted.
Great article Justin, this is a useful overview.
Kirill
great post! Great for referencing the different types and seeing some quick examples.
Thanks!
Very nice article, especially the graphics. What a nice introduction to these concepts.
Hi Justin,
you mention that ‘[quote]SortedDictionary doesn’t allow indexed access[/quote]’ but in the example you ‘get key by index’ and also ‘get value by index’. MSDN also states that there is no indexed retrieval with SortedDictionary, but I don’t get it. Could you please clarify?
Thank you!
Juraj
@Juraj Good catch, I’m not sure how those got in there. The Keys and Values properties on the SortedDictionary do not allow access by index.
In System.Collections.Generic.Dictionary<TKey,TValue>
the comment // lookup by index should be // lookup by key
@labilbe Thanks!
Just came across this post, Justin – it’s great! I’m sharing it around the developers at my office, as a handy cheatsheet to save us from gaffes like using a dictionary to simulate a set, or a list to simulate a queue. Nice one!
Great post! thumbsup! 😀
Ur the man. Best Collection.Generics overview on the web.
Thanks for the great overview about the runtime behavior of the different collections.
Does someone know about an good overview about the memory consumption similar to the Bottom line overview?
Thanks in advance
ThiasG
Thank you for this post, specifically taking the time to make it really useful.
Hey Justin, thanks for the great write up, this is a valuable resource! One question though: you say that to insert into the SortedList, “the entire array has to be shifted in order to make room for the new item”, and essentially seem to be saying that the implementation is an array under the hood. However, according to MSDN, this class is “is a binary search tree”. (http://msdn.microsoft.com/en-us/library/ms132319%28VS.80%29.aspx)
Do you happen to know if this is a mistake here or on MSDN, or has something perhaps changed in the BCL?
Many thanks for clearing up this confusion!!