Introduction to the new .net 3.5 HashSet class

In the .net 3.5 framework we now have a typesafe class specifically engineered for high performance set operations. The HashSet class is so useful when performing set operations on groups of objects that I just had to share it. If you are not familiar with set theory, I will give you a quick overview. First, a set is just a group of objects. So, here is our set:

The first operation that we will perform on the set is an intersect. An intersection is the set of items in two overlapping sets. For example:

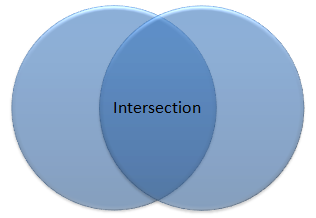
Here we have two overlapping sets, the intersection is the items that are in both sets. The next operation that we are going to look at is a union. A union is the combination of all items in two sets.

Here the Union is all items in both sets, including that items that are only in one of the sets. The next concept is a subset. A subset is a set that is comprised of items that are all in another set. For example:

By definition a set is automatically a subset of itself, since all of its items are contained in itself. So, we have something called a "proper subset" which is a subset that is not equal to itself. The set shown in the picture above would be a proper subset. This leads us to the concept of a Superset, which is the opposite of a subset:

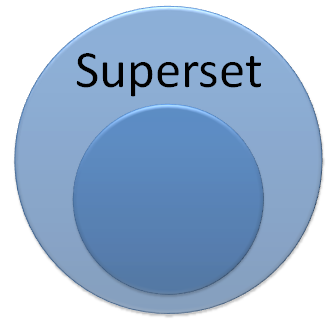
There is also a "proper superset" which is just a superset that is not equal to itself. So, now that we have gotten some quick set operations out of the way, lets look at the HashSet class and how we would go about using it to do these things. First we will look at an intersection:

  var stringSet1 = new HashSet<string> { "John", "Mike", "Fred" };

  var stringSet2 = new HashSet<string> { "Bob", "Ted", "John" };

  stringSet1.IntersectWith(stringSet2);

First of all we are using a collection initializer to setup our hashsets and then I call IntersectWith which leaves stringSet1 with just a single item "John". Next we will do a union:

  var stringSet1 = new HashSet<string> { "John", "Mike", "Fred" };

  var stringSet2 = new HashSet<string> { "Bob", "Ted", "John" };

  stringSet1.UnionWith(stringSet2);

This will leave stringSet1 with "John", "Mike", "Fred", "Bob", and "Ted". Notice that "John" is not in there twice, any duplicates are removed in a Union operation because in a true union operation two items that have the attributes are considered to be the same. In this case the two strings are equal and therefore they are considered to be the same. Next we will look at the subset and superset methods:

  var stringSet1 = new HashSet<string> 

    { "John", "Mike", "Fred", "Bob", "Ted" };

  var stringSet2 = new HashSet<string> { "John", "Bob" };

  stringSet1.IsProperSupersetOf(stringSet2); //true

  stringSet2.IsProperSubsetOf(stringSet1); //true

  stringSet1.IsProperSubsetOf(stringSet2); //false

  stringSet1.IsSubsetOf(stringSet1); //true

  stringSet1.IsSupersetOf(stringSet1); //true

They correlate directly to the set operations and work exactly as expected. I’m not going to go through each one since we already went over the functions above. They also provide an "ExceptWith" method:

  var stringSet1 = new HashSet<string> 

    { "John", "Mike", "Fred", "Bob", "Ted" };

  var stringSet2 = new HashSet<string> { "John", "Bob" };

  stringSet1.ExceptWith(stringSet2);

This returns the set "Mike", "Fred", and "Ted". This method just removes all of the items in the second set from the first set. The HashSet class also provides an "Overlaps" method that tells us if a second set has any items in common with the current set. There is a "SetEquals" method that allows us to determine if the first set is equal to the second set. The last two methods that we are going to look at is "SymmetricExceptWith" and "RemoveWhere". "SymmetricExceptWith" simply returns all items in both sets except the items in common:

  var stringSet1 = new HashSet<string> 

    { "John", "Mike", "Fred", "Bob", "Ted" };

  var stringSet2 = new HashSet<string> { "John", "Bob", "Scott" };

  stringSet1.SymmetricExceptWith(stringSet2);

This operations leaves set 1 with "Mike", "Fred", "Scott", and "Ted". "John" and "Bob" a removed since both sets share the item. Next we have "RemoveWhere" which allows us to remove items that match our expression:

  var stringSet1 = new HashSet<string> 

    { "John", "Mike", "Fred", "Bob", "Ted" };

  stringSet1.RemoveWhere(x => x.StartsWith("F"));

In this case since we are using strings I can call "StartsWith" and therefore we end up with stringSet1 containing "John", "Mike", "Bob", and "Ted".

So, there you have it. This post ended up a little like a page out of a textbook, but I guess sometimes we just have to grin and bear it. The HashSet class is just so useful in so many ways that I just had to expose people to it. None of these operations are incredible difficult, but now we have a build in class that we can always count on being there. Enjoy!