Multi-Threaded K-Means Clustering in .NET 4.0

A little while back I gave a presentation on the some of the new parallel features of .NET 4.0. One of the demos I had prepared was a K-Means clustering application since it provided an embarrassingly parallel algorithm to show off the power of the new parallel libraries. Recently I was going through some of my directories and I saw the demo folder and I realized that I had never posted it up on my blog! So that is what I am going to do today.

Explaining the K-Means Clustering Algorithm

The K-Means clustering algorithm is really quite simple. It is all about taking a set of items and then placing them in an arbitrary number of groups according to their “distance” from each other. In order to explain the algorithm, I am going to start off with a very simple example in a 2 dimensional plane. First we start off with a bunch of points in our plane:

The first step is for us to decide how many clusters we want (this is the “k” in “k-means”). In this case, we will just pick 3. The next step is to choose three spots at random.

Once we have our three spots we assign all of the points into one of the groups based on their distance from the different points:

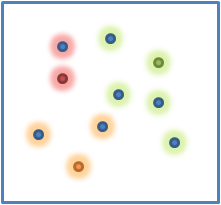
Next, we take each point within each cluster and we calculate the centroid. Once we have the centroid, it becomes our new center. Then we repeat the process:

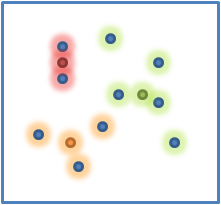
Once the centroids are calculated, then we again assign all points to a center based on their distance. If we repeat this process of calculating the centroid and shifting the center of the group then the centroids will eventually converge and stop moving. This is when we know that we have the groups. In the diagrams above, since no points moved between groups when we calculated the centroids then when we calculate the centers again, they won’t move. At this point we say that the centroids have converged and we now have our calculated groups.

Breaking It Down

Here are the steps that we are going to go through:

1. Create Random Points
2. Pick Random Center Points
3. Assign Points To Centers
4. Calculate New Centers
5. Check If Centers Are Equal (if so, quit)
6. Go To 3

The two steps that I have put in bold are the ones where we are going to more easily be able to exploit parallelism. In step 3, we are going to loop over every point and determine which center is closest to it. Since there is no state modified during this lookup, we can easily make this process parallel. In step 4, when we calculate new centers, we are just going to loop over all of the points in a given group and calculate their “average” location (or centroid).

For step 3, all we need to do is loop through each point and check every center until we find the closest one. If we weren’t concerned with writing a parallel application then we could simple loop over them with a normal foreach statement:

foreach (var point in Points){
    //content goes here
}

But if we leverage the System.Threading.Tasks.Parallel class in .NET 4.0, we could simply write this:

Parallel.ForEach(points, point => {
    //contents goes here
});

And with that one simple change, we have now made our loop parallel. We have to keep in mind that we still need to implement locking if we share any state between loops.

That is pretty neat, but instead of using a loop, we could have also used Linq to loop over the list (using a customer “ForEach” extension method):

points.ForEach(point => {
    //contents go here
});

Thankfully, .Net 4.0 also provides us with Parallel Linq! The System.Linq.ParallelEnumerable class provides a method called “ForAll” which loops over every item in a list. This means that we can just use the “AsParallel” extension method and perform the exact same operation:

points.AsParallel().ForAll(point => {
    //contents go here
});

Phew! That sure was hard. All we have to do for the center calculations is the exact same thing. Before we know it, we have increased the performance of our application by a huge amount. On my dual core laptop I get an almost linear speed-up when I turn off drawing to the screen. Unfortunately the drawing on the screen eats up way more CPU than the calculations.

Looking At The Demo

The application starts off like this:

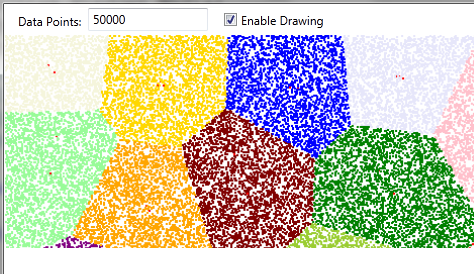
And then ends like this:

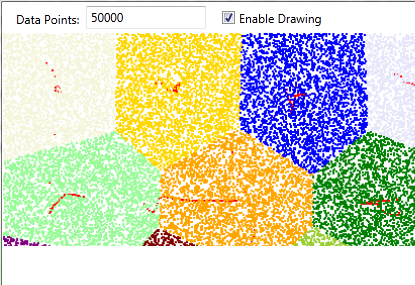
You can see where the centers migrated and the groups came to form more regular shapes. The same set of randomly generated points are run twice, once with a single thread and then again using the parallel features in .NET 4.0.

What Use Is This To Me?

Well, in this case we are simply grouping together 2-dimensional points, and so when we say distance we are talking about basic euclidean distance:

Image via Wolfram Alpha.

But what if we weren’t grouping points? What if we had a bunch of strings? We could certainly use a string based distance metric, for example Levenshtein distance. Or what if we had products? We could make price the similarity metric and calculate distance between products be merely their difference in price. Or we could base “distance” on a number of factors. As long as we have a way to calculate distance between two items in your set, then you can apply K-Means clustering.

Get The Source

Keep in mind that this is a demo app, and the code is not production code. You’ll probably ignore me and put it in production anyways, but I thought I’d at least put the disclaimer somewhere in here.

If you want to check out the application, and you have VS2010 installed, you can grab it below. If anyone has some time and wants to go over the application and speed it up more or clean it up, please do! I’ll repost it with credit (obviously). The interesting tidbits are in the KMeansWorker class.

Get The Source

Summary

I hope you found this at least interesting, if not useful. Thanks!